Natural Frequency and Resonance Products and their sub-components, as well as packaging materials and structures possess what is called natural frequency.
In the simplest of terms, natural frequency is where those items like to vibrate – or get excited - whenever they are mechanically disturbed. As with the Part 2 email, I like to reference sound to help describe vibration in more simple terms.
If you think of a tuning fork, it is specifically designed and manufactured to respond at a specific, discreet frequency. Whether you hit that tuning fork with a hammer, a stick, or a spoon, it’s going to respond with the same frequency tone (sound), regardless.
The amplitude/intensity of the sound may be different for each, but the frequency/tone will be the same. Another way we describe vibration response is in terms of a simple spring-mass system. The natural frequency (f) response of a spring-mass system is related to the mass (m) of the item, as well as the spring constant (k – think stiffness) of the spring. We describe that relationship with the formula as shown below.
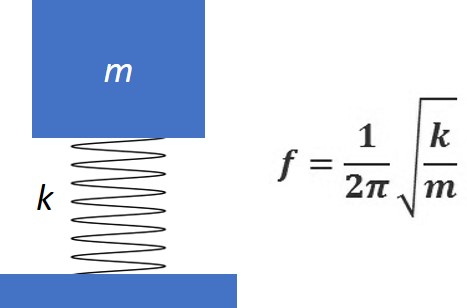
Determining Product Natural Frequency You can think of a product being made up of what are potentially many different spring-mass systems - depending on the product's complexity. To determine test item natural frequency, we use Vibration Test Systems in the laboratory to perform what are called sinusoidal sweeps.
Since this discussion is focused on concerns with transport vibration, this helps to define both the low and high ends (the range) of our frequency sweeps. ASTM D3580 - Standard Test Methods for Vibration (Vertical Linear Motion) Test of Products, helps to define the step-by-step procedure used for this type of testing. D3580 defines the sweep frequency range by indicating “Experience has shown that most individual transportation environments contain frequencies ranging from 3-100 Hz.”
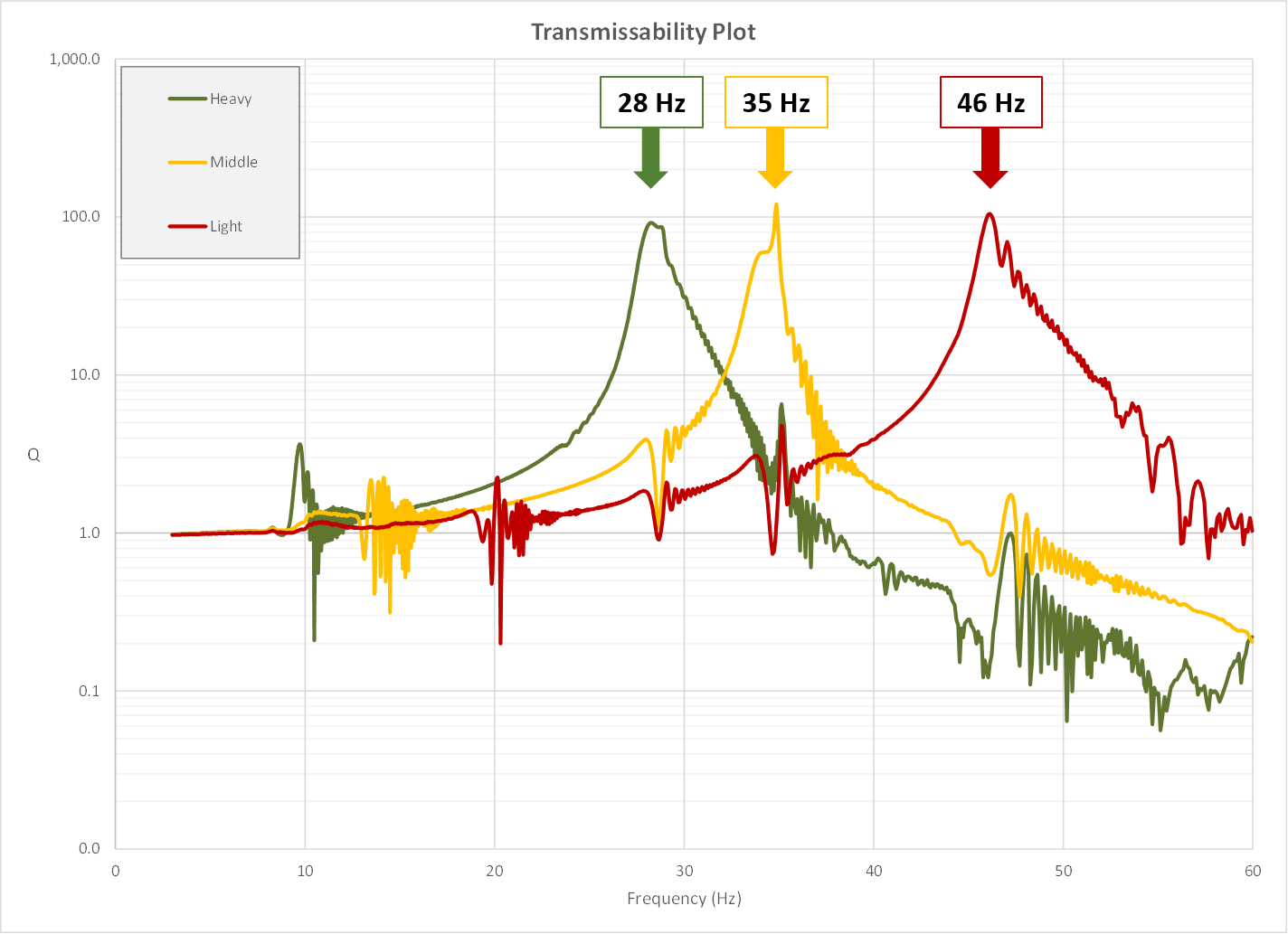
Though it’s true the most significant amplitude of transport vibration input occurs in that 3-100 Hz. range, environmental transport measurement studies have shown a more comprehensive frequency range is better defined as 2-200 Hz. For demonstration, we placed three tuned spring-mass systems on a Lansmont Vibration Test system and performed sine sweeps between 3-100 Hz. The only differences between each of the spring-mass systems were the masses attached to the springs. The spring constants were the same.

Considering the formula described in Figure 1, we could assume that the heavy mass would have the lowest natural frequency, and the light mass would have the highest natural frequency. In fact, if we attach an accelerometer to each of the masses while performing the sweep, we’re able to quantitatively measure each of their individual responses.
During a sine sweep, we’re controlling the table with a predefined, constant input amplitude, then measuring the response from each of our spring-mass systems. If we divide the response signal by the input signal, we create what is called a transmissibility value - or what is sometimes referred to as Q. As an example, if I’m controlling the table with a constant 0.5g input, while simultaneously measuring a response on one of the masses at 1.0g, then I have a transmissibility of 2 (response/input).
If we measure and compare the table input to each of the three spring-mass systems, we create a transmissibility plot that looks like that below.
Considering the formula described in Figure 1, we could assume that the heavy mass would have the lowest natural frequency, and the light mass would have the highest natural frequency. In fact, if we attach an accelerometer to each of the masses while performing the sweep, we’re able to quantitatively measure each of their individual responses.
During a sine sweep, we’re controlling the table with a predefined, constant input amplitude, then measuring the response from each of our spring-mass systems. If we divide the response signal by the input signal, we create what is called a transmissibility value - or what is often referred to as Q. (Note Q is truly defined as the ratio of the resonant frequency to the bandwidth of amplification range. The higher the Q value, the more narrow, or sharp the resonant bandwidth.
Conversely, the lower the Q value, the more wide/broad the resonant bandwidth). As an example, if I’m controlling the table with a constant 0.5g input, while simultaneously measuring a response on one of the masses at 1.0g, then I have a transmissibility of 2 (response/input). If we measure and compare the table input to each of the three spring-mass systems, we create a transmissibility plot that looks like that below.
Sine Sweep and Resonance Search in 1-minute from Lansmont Corporation on Vimeo.
This sinusoidal sweep test is more of an Engineering exercise - not a test-to-failure, and not a pass/fail test. While sweeping between the defined lower and upper frequencies, we do so at a constant amplitude.
The amplitude of the vibration is set just high enough to excite the test structure(s), but not so high that it will cause any failures. The goal of the test is primarily to understand how the product/component/packaging responds to controlled inputs across a given frequency range.
What do we do with this natural frequency and transmissibility information? When packaged products are moving through the distribution environment, they will experience vibration, including input that spans those natural frequency ranges.
There’s simply no avoiding it. Luckily, protective packaging can be engineered (tuned) to mechanically filter, or attenuate transport input vibration that occurs at, or near the product’s natural frequency, versus potentially amplifying the input. In Part 4, we’ll provide some demonstrable examples that show how use of product transmissibility data was used to help design and tune a cushioned transport solution, in an effort to eliminate vibration-related transport damage.